Bilangan berpangkat dan bentuk Akar (BAB I)

Bilangan berpangkat
pangkat suatu bilangan adalah perkalian suatu bilangan secara berulang dengan bilangan itu sendiri
Bentuk : Aⁿ = a x a x … x a = b
a : bilangan pokok
n : pangkat
b : hasil dari perpangkatan

Rumus
A^m x aⁿ = a^m+n A^m : aⁿ = a^m/ aⁿ = a^m-n (a^m)ⁿ = a ^mxn (axb)^m = a^m x b^m (a.b)ⁿ = aⁿ/bⁿ A⁰=1
Contoh : -2⁴ =  -2 x -2 x -2 x -2 = 16 -(2)⁴ = -(2.2.2.2)= -16
(2/3)³ = 2/3 x 2/3 x 2/3 = 8/27
Nilai operasi perpangkatan  Contoh :

Akar

Pola Barisan dan Deret (BAB II)
pola bilangan dapat diartikan sebagai susunan bilangan yang memiliki keteraturan. Dalam matematika dikenal beberapa jenis pola bilangan antara lain:

• Pola bilangan ganjil adalah 1,3,5,7.  Rumus urutan ke-n adalah 2n-1 dan jumlah bilangan n adalah n^2.

• Pola bilangan genap adalah 2,4,6,8. Rumus urutan ke-n adalah 2n dan jumlah dari n bilangan genap adalah n(n + 1)
• Pola bilangan segitiga adalah 1,3,6,10. Rumus urutan ke-n n(n+1)/2

• Pola bilang persegi adalah 1,4,9,16. Rumus urutan ke-n adalah  ⁿ²

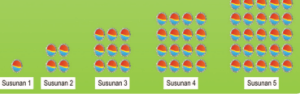
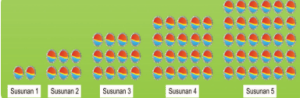
• Pola bilangan persegi panjang 2,6,12,20. Rumus urutan ke-n adalah n(n+1)

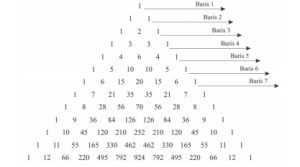
• Setiga pascal. Rumus jumlah bilangan baris ke-n adalah  2^n-1

Suku ke-n suatu barisan bilangan

Rumus suku ke-n adalah Un= a+ (n-1)b a = U1 : suku pertama Un = Suku ke- n n : banyak suku b= Un-Un-1= beda antara 2 suku berurutan
Suku tengah deret Aritmatika Ut = U1 + Un/2 Ut : suku tengah U1 : Suku pertama Un : suku ke-n
Jumlah n suku pertama deret Aritmatika Sn= 1/2 x n  ( U1 + Un)

                       atau 
Sn= 1/2 x n ( 2U1 +(n-1)b)
Deret geometri deret geometri adalah deret dengan rasio antar 2 suku yang berurutan selalu tetap.

Jumlah n suku pertama deret geometri Sn =  U₁ (rⁿ-1)/ r-1 Sn : Jumlah suku pertama U1 : Suku pertama r : rasio n : banyak suku